1
Excerpts from this work may be reproduced by instructors for distribution on a not-for-profit basis
for testing or instructional purposes only to students enrolled in courses for which the textbook
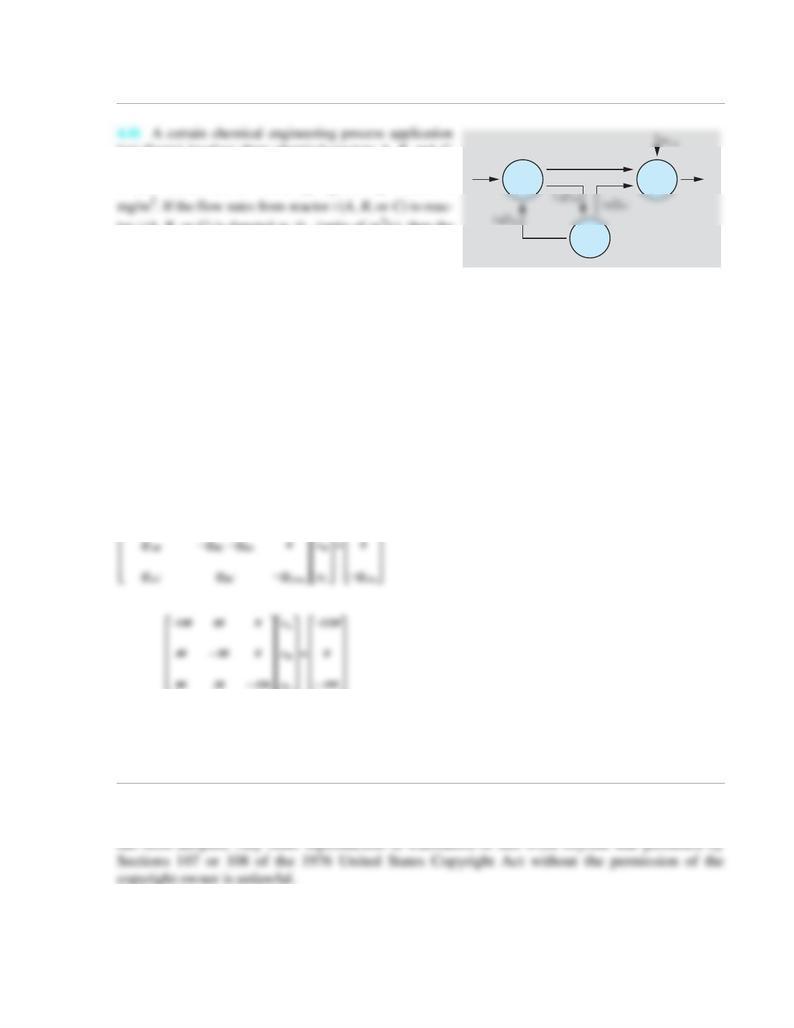
(see figure) involves three chemical reactors A, B, and C.
At steady state, the concentrations of a particular species n
in each reactor has the values , , and in units of
tor j (A, B, or C) is denoted as (units of m3/s), then the
mass flow rate of species n from reactor i to reactor j is
(units of mg/s). Since this chemical species is con-
served (i.e., neither produced nor destroyed) conservation of mass (of the species) for each reactor must
hold. For the process shown in the figure, m3/s, m3/s, m3/s,
m3/s, m3/s, mg/s, and mg/s. Write down the mass con-
tinuity equations for each reactor and solve them to find the concentrations , , and in each reactor.
Solution
Conservation of mass yields:
QAin+xBQBA-xAQAC-xAQAB = 0
xAQAB-xBQBC-xBQBA = 0
QCin+xBQBC+xAQAC-xCQCout = 0
which yields:
Solution with MATLAB:
>> A=[-140 60 0; 40 -80 0; 80 20 -150];
A
A
B
C
x
A
Q
AC
m
Ain
x
C
Q
Cout
xA
xB
xC
Qij
xiQij
QAB 40=
QAC 80=
QBA 60=
QBC 20=
QCout 150=
mCin 195=
mAin 1320=
xA
xB
xC
−
−−
Ain
A
BAABAC
Q
x
0QQQ
−
C

2
>> B=[-1320; 0; -195];
>> x=A\B
x =
8.5000e+00
The solution is xA= 12 mg/m3, xB= 6 mg/m3, xB = and 8.5 mg/m3.